Κατηγορία: Άλγεβρα

Για να ορίσουμε τη λογαριθμική ή ισογώνια σπείρα θα χρειαστούμε εξισώσεις που λέγονται παραμετρικές. Ένα γράφημα όπως το παρακάτω, που αντιστοιχεί σε λογαριθμική σπείρα δεν μπορεί να εκφραστεί με εξίσωση της μορφής y=f(x) γιατί δεν αποτελεί συνάρτηση.

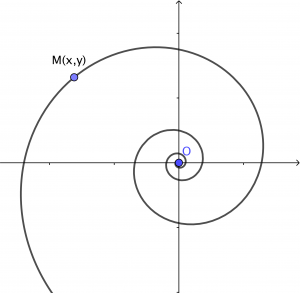
Θυμηθείτε ότι στις συναρτήσεις πρέπει οι κατακόρυφες ευθείες να τέμνουν το γράφημα σε ένα το πολύ σημείο κάτι που δεν συμβαίνει εδώ. Για να ξεπεραστεί το πρόβλημα πρέπει να εισάγουμε μια νέα μεταβλητή  που λέγεται παράμετρος. Αν υποθέσουμε ότι μια καμπύλη όπως το σχήμα εκφράζει την τροχιά ενός σωματιδίου M που κινείται στο επίπεδο, τότε οι συντεταγμένες θέσης του σωματιδίου ως συνάρτηση της μεταβλητής t (που συνήθως είναι ο χρόνος) εκφράζονται με ένα ζεύγος εξισώσεων x=f(t) και y=g(t) που λέγονται παραμετρικές. Συνεχίστε την ανάγνωση του “Λογαριθμική σπείρα.”