Για να ορίσουμε τη λογαριθμική ή ισογώνια σπείρα θα χρειαστούμε εξισώσεις που λέγονται παραμετρικές. Ένα γράφημα όπως το παρακάτω, που αντιστοιχεί σε λογαριθμική σπείρα δεν μπορεί να εκφραστεί με εξίσωση της μορφής y=f(x) γιατί δεν αποτελεί συνάρτηση.
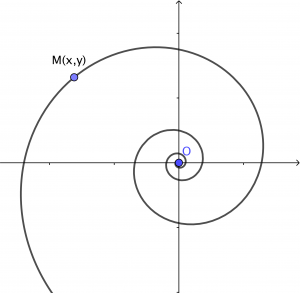
Θυμηθείτε ότι στις συναρτήσεις πρέπει οι κατακόρυφες ευθείες να τέμνουν το γράφημα σε ένα το πολύ σημείο κάτι που δεν συμβαίνει εδώ. Για να ξεπεραστεί το πρόβλημα πρέπει να εισάγουμε μια νέα μεταβλητή που λέγεται παράμετρος. Αν υποθέσουμε ότι μια καμπύλη όπως το σχήμα εκφράζει την τροχιά ενός σωματιδίου M που κινείται στο επίπεδο, τότε οι συντεταγμένες θέσης του σωματιδίου ως συνάρτηση της μεταβλητής t (που συνήθως είναι ο χρόνος) εκφράζονται με ένα ζεύγος εξισώσεων x=f(t) και y=g(t) που λέγονται παραμετρικές.
Οι παραμετρικές εξισώσεις της λογαριθμικής σπείρας είναι:
x(t)=α eβt συνt
y(t)=α eβt ημt
όπου α, β είναι πραγματικοί αριθμοί που σχετίζονται με τη μορφή της.
Η λογαριθμική σπείρα περιγράφηκε για πρώτη φορά από τον Rene Descartes και αργότερα ερευνήθηκε εκτενώς από τον Jacob Bernoulli. Ο Bernoulli ενθουσιάστηκε τόσο πολύ με τις ιδιότητές της που την ονόμασε spira mirabilis (θαυμάσια σπείρα). Μάλιστα ζήτησε να την σκαλίσουν στο μνήμα του με την επιγραφή “Eadem mutata resurgo”, που σε ελεύθερη μετάφραση σημαίνει “αν και έχω αλλάξει θα ξαναπάρω την ίδια μορφή”, εξ αιτίας της ιδιότητας που έχει αν την μεγεθύνουμε, το σχήμα της δεν θα αλλάξει αλλά θα είναι ένα ακριβές αντίγραφο του εαυτού της, αν και ο καλλιτέχνης από λάθος ίσως, σχεδίασε μια σπείρα του Αρχιμήδη και όχι τη λογαριθμική.
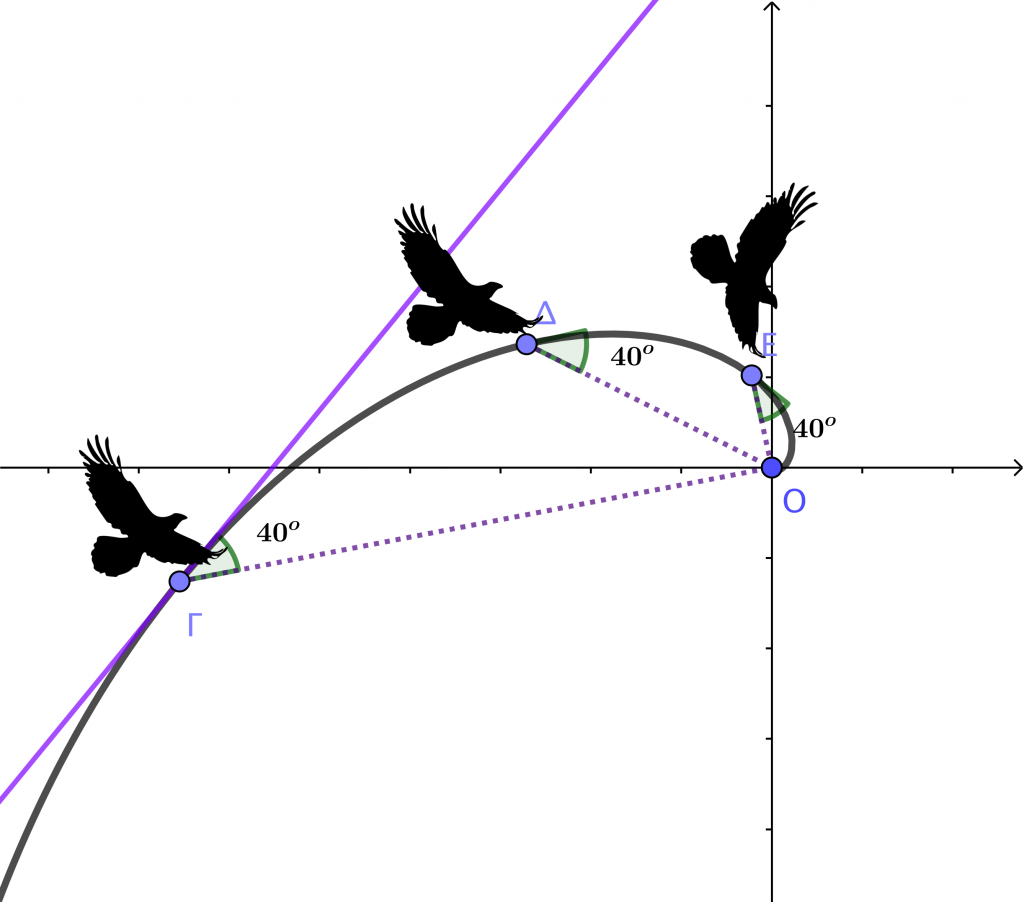
Παρακάτω θα βρείτε μια μικροεφαρμογή GeoGebra για τη λογαριθμική σπείρα όπου μπορείτε να μεταβάλλετε τις παραμέτρους α, β και να δείτε την επίδραση που έχουν σ΄ αυτή. Επιλέγοντας το κουτί “εφαπτομένη” θα ανακαλύψετε μια σημαντική ιδιότητα που έχει: η εφαπτομένη της σπείρας σε οποιοδήποτε σημείο της Α, σχηματίζει με το ευθύγραμμο τμήμα ΟΑ σταθερή γωνία, γι αυτό και το όνομα ισογώνια. Μετακινήστε το σημείο Α για να το διαπιστώσετε. Αν το σημείο Α δεν εμφανίζεται στην οθόνη σας αλλάξτε την τιμή της παραμέτρου α για να εμφανιστεί.
Μετάβαση σε πλήρη οθόνη της εφαρμογής.
Πετώντας σε μια λογαριθμική σπείρα.
Τα γεράκια χρησιμοποιούν δύο δεξιότητες για να επιτεθούν στο θήραμά τους, την ταχύτητα πτήσης και την οπτική τους οξύτητα. Για να επιτύχουν μικρότερη αεροδυναμική αντίσταση και άρα μεγαλύτερη ταχύτητα πρέπει να έχουν το κεφάλι τους ευθυγραμμισμένο με τον κορμό τους αλλά αυτό τους στερεί σε οπτική οξύτητα γιατί η βέλτιστη όραση γίνεται με το βαθύ βοθρίο των οφθαλμών τους που είναι προσανατολισμένο σε γωνία 40 μοιρών περίπου από τον άξονα της κεφαλής. Για να μην αναγκαστούν να γυρίσουν το κεφάλι κατά την πτήση για να δουν καλύτερα και άρα χάσουν σε ταχύτητα, δεν επιτίθενται σε ευθεία πορεία, αλλά κατά μήκος μιας λογαριθμικής σπείρας εκμεταλλευόμενα την ιδιότητα της σταθερής γωνίας της εφαπτομένης που διαπιστώσατε παραπάνω.
Το πρόβλημα των τεσσάρων σκαθαριών.
Ας υποθέσουμε ότι έχουμε τέσσερα σκαθάρια στις τέσσερις κορυφές ενός τετραγώνου και ότι το ένα προσπαθεί να πιάσει το σκαθάρι που βρίσκεται στην επόμενη κορυφή. To A κυνηγάει το Β, το Β κυνηγάει το Γ κλπ. Ποια θα είναι η πορεία των σκαθαριών; Αρχικά τα σκαθάρια θα κινηθούν κατά μήκος των πλευρών του τετραγώνου αλλά για πολύ λίγο αφού το σκαθάρι στόχος θα έχει φύγει από την κορυφή που βρισκόταν πριν. Έτσι θα αλλάξουν διεύθυνση και θα κινηθούν πάνω στις πλευρές ενός άλλου εσωτερικού τετραγώνου αλλά και πάλι για πολύ λίγο. Τελικά οι πορείες τους θα συγκλίνουν στο κέντρο και θα είναι λογαριθμικές σπείρες. Το ίδιο θα συμβεί αν τοποθετήσουμε τα σκαθάρια στις κορυφές οποιουδήποτε άλλου κανονικού πολυγώνου.
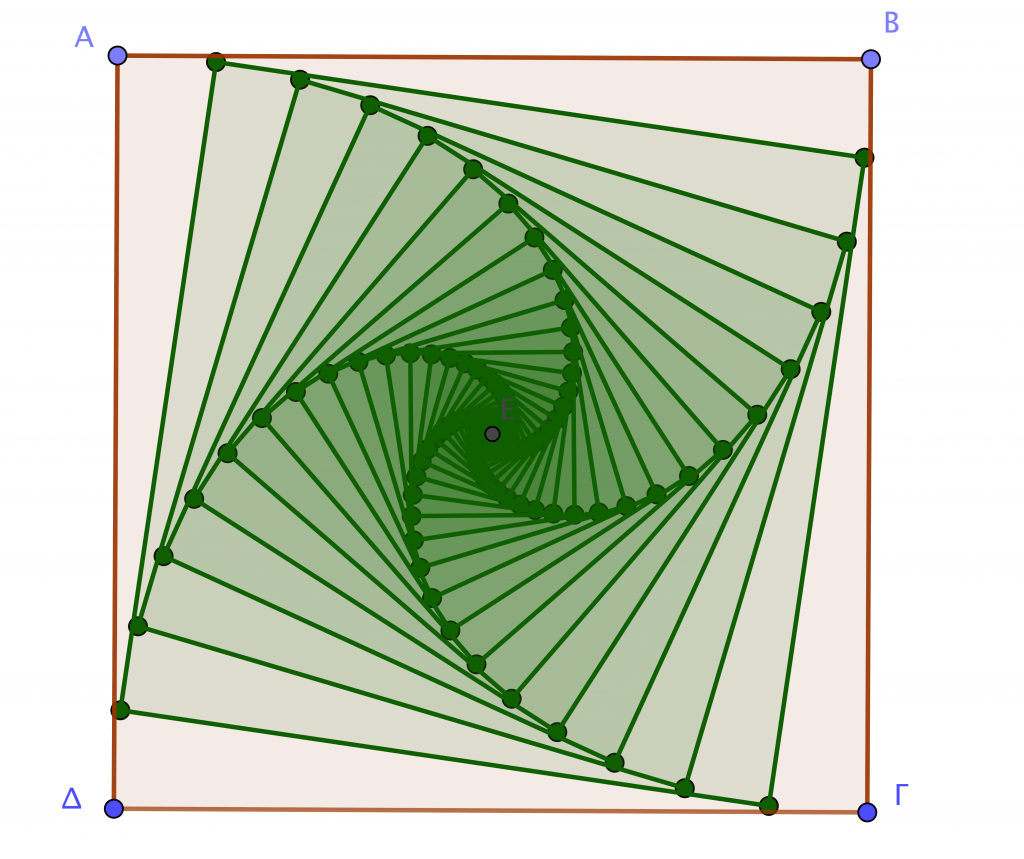
Μήπως μπορείτε να βρείτε τη σταθερή γωνία των σπειρών στην περίπτωση του τετραγώνου;
Εφαρμογές της λογαριθμικής σπείρας.
 |
 |
 |
 |
 |
| Ναυτίλος | Μπρόκολο ρομανέσκο | Ηλιοτρόπιο | Κυκλώνας | Σπειροειδής γαλαξίας |
Πηγές:
https://en.wikipedia.org/wiki/Logarithmic_spiral
http://mathworld.wolfram.com/LogarithmicSpiral.html